首页 > 常识 >
三次二项式的定义(二项式定理的基本概念)
100次浏览 发布时间:2024-10-30 10:36:15一、二项式定理的基本概念
我们首先要明确"二项式"的概念。简单说,用"a+b"表示的式子叫做二项式。或者说二项式是只有两项的多项式,即表示两个单项式a+b的和,它也是最简单的多项式。
下面重点解读二项式定理的基本概念
用文字语言来描述二项式定理的基本概念:
应用组合的知识研究二项展开式中的系数规律,并写成一般的展开公式,这个公式叫做二项式定理。
用符号语言描述二项式定理的概念:
(a+b)^n]=Cvn0a^n]+Cvn.1]
avn-1b…Cⅴnk]a^n-k]…
Cvnn]b^n
二、二项式定理展开式各项系数的规律与内在联系
我们先利用二项式的三次幂来分析它展开式各项的系数规律:
(a+b)^3]=a^3]+3a²b+3ab²+
b^3
这里需要先说明一点,如果是二项式的3次幂,它的展开式就是四项多项式。二项式的四次4次幂,它的展开式就是五项的多项式。如果是二项式的n次幂,它的展开式则是n+1项的多项式。注意二项式是奇次幂,它的展开式共有偶数项。如果二项式是偶次幂,它的展开式共有奇数项。
我们看二项式的三次幂,它的展开式是四项多项式。它系数的规律,首项a的系数是1,它的次数是3。第二项ab的系数是3,a的次数是2,b的次数是1。第三项ab的系数还是3,a的次数是1,b的次数是2。第四项也是尾项b,它的系数是1,次数是3。所以二次三项式可以写成下面的形式,即:
(a+b)^3=cv3.0]a^3+c^3.1]3a²b+cv3.2]3ab²+cv3.3]b^3
由此我们看到二项式的三次幂,它的展开式各项系数的规律。首项a和尾项b的系数都是1,它们的次数各是3。实际上就是二项式二次幂展开式的首项和尾项的系数1。第二项ab的系数,则是二项式二次幂展开式的首项系数1与第二项系数2的和。第三项ab的系数是2与1的和。2与1是谁,同学们都知道,在这里就不多说了。
(a+b)^3这是个特式,它的一般式子可以规纳为:
(a+b)^n]=cⅴn0a^n]+cvn^1]a^
n-1]b…+cⅴnk]a^n-k]+…
cⅴnn]b^n
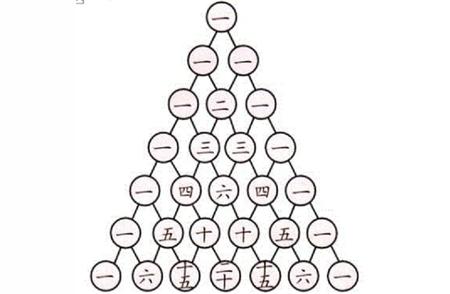
这个一般式子的展开式,它的各项系数规律就是我们说的"杨辉三角"。
同学们参看"杨辉三角"图形,按着系数规律,自己确定出二项式的4次幂,和二项式的5次幂展开式的各项系数。
下面我再简要的介绍一下二项式的n次幂展开式的各项系数的规律。
展开式的各项系数是有一定规律的,我们看"杨辉三角"图。图形的第一行是1,第二行是1,1。第三行的首数是1,第二位数是2,正是第二行两个1的和,第三位数还是1,…,它是三角形的形状,简称"杨辉三角"。杨辉三角实际上就是二项式定理展开式各项系数的规律和它内在联系。关于二项式n次幂的展开式各项系数的规律,就简要的解读到这里。
三、通项公式
关于通项公式在这里还要做点提示,注意这里的通项不是指展开式中的第k项,而是指第k+1项,用Tⅴk+1表示二项展开式中的第几项。通项公式用符号语言描述如下:
丅ⅴk+1]=Cvn.k]a^n-k]b^k
四、注意一些常用名词术语
我们还要强调一点,学习二项式定理要注意以下一些名词述语。
2x2x2这是原式,这个原式也是繁写,2^3这是原式的简写。αb+ab是原式,也是繁写。把这个繁写的原式变形为简写的式子则为2αb,2αb也是这个二项式的和,也是这个二项式的因式。注意加法的简写也是把多项式进行因式分解。多项式又叫做因式的展开式,展开式的简写是因式,也叫做分解因式。把因式展开,实际上是把因式进行繁写,也是把乘法写成加法的形式。
还要注意,二项式n次幂的展开式,先考虑首项的系数,再考虑首项的次数。
展开式中的第二项ab,还是首先考虑ab的系数,再考虑ab每个因式的次数。…
注意"原式变形"与"形变值不变"等常用词语,这些专用词语在老师讲课的过程中经常用到
相关文章
- 德凌联邦保险柜全国统一服务热线-全国24小时服务中心实时反馈全+境+到+达(德凌联邦保险柜保险柜报警怎么解除) 09-15
- 帛思绮保险柜维修服务中心|全天24小时服务热线实时反馈全+境+到+达(帛思绮保险柜保险柜怎么样) 09-14
- 稳东保险柜-全国各售后热线实时反馈全+境+到+达(稳东保险柜保险柜没电了怎么开) 09-14
- 航通保险柜售后号码多少实时反馈-今-日-资-讯(航通保险柜保险柜怎么样) 09-14
- 枫林湾保险柜服务号码-故障报修热线号码实时反馈-今-日-更-新(枫林湾保险柜文件保险柜怎么打开) 09-14
- 艾谱(AIPU)保险柜/全国各市服务热线号码实时反馈-今-日-更-新(艾谱(AIPU)保险柜保险柜报警怎么解除) 09-14
- 骄鹿保险柜热线服务维修400客服24小时客户报修热线(骄鹿保险柜保险柜怎么搬运) 09-14
- 京酷保险柜24小时人工服务24小时客服全国各售后受理客服中心(京酷保险柜保险柜的密码怎么改) 09-14

